The Nature of Covalent Bonding 82 Section Review

Condensed Matter Physics

64 Types of Molecular Bonds

Learning Objectives

Past the cease of this department, you will be able to:

Distinguish between the different types of molecular bonds
Determine the dissociation free energy of a molecule using the concepts ionization energy, electron affinity, and Coulomb force
Describe covalent bonding in terms of exchange symmetry
Explain the physical structure of a molecule in terms of the concept of hybridization

Quantum mechanics has been extraordinarily successful at explaining the construction and bonding in molecules, and is therefore the foundation for all of chemistry. Quantum chemistry, equally it is sometimes chosen, explains such basic questions as why ${\text{H}}_{2}\text{O}$ molecules exist, why the bonding angle between hydrogen atoms in this molecule is precisely $104.5\text{°}$ , and why these molecules bind together to form liquid water at room temperature. Applying quantum mechanics to molecules tin exist very difficult mathematically, then our discussion will be qualitative only.

As we study molecules and and then solids, nosotros will employ many different scientific models. In some cases, we expect at a molecule or crystal every bit a set of point nuclei with electrons whizzing around the exterior in well-defined trajectories, as in the Bohr model. In other cases, we utilise our full knowledge of quantum mechanics to study these systems using wave functions and the concept of electron spin. It is important to recollect that nosotros written report modern physics with models, and that different models are useful for different purposes. We do not e'er utilize the nigh powerful model, when a less-powerful, easier-to-employ model will do the chore.

Types of Bonds

Chemical units form by many unlike kinds of chemical bonds. An ionic bond forms when an electron transfers from 1 atom to another. A covalent bond occurs when 2 or more atoms share electrons. A van der Waals bail occurs due to the attraction of charge-polarized molecules and is considerably weaker than ionic or covalent bonds. Many other types of bonding be as well. Oftentimes, bonding occurs via more than one mechanism. The focus of this section is ionic and covalent bonding.

Ionic bonds

The ionic bond is perhaps the easiest type of bonding to sympathize. It explains the formation of salt compounds, such as sodium chloride, NaCl. The sodium atom (symbol Na) has the same electron organization as a neon atom plus ane iiisouthward electron. Simply 5.fourteen eV of energy is required to remove this ane electron from the sodium atom. Therefore, Na tin can easily surrender or donate this electron to an adjacent (nearby) atom, attaining a more than stable organisation of electrons. Chlorine (symbol Cl) requires just one electron to consummate its valence shell, so it readily accepts this electron if it is almost the sodium cantlet. We therefore say that chlorine has a large electron affinity, which is the energy associated with an accepted electron. The energy given up past the chlorine atom in this process is three.62 eV. Afterward the electron transfers from the sodium atom to the chlorine atom, the sodium atom becomes a positive ion and the chlorine atom becomes a negative ion. The total energy required for this transfer is given by

${E}_{\text{transfer}}=5.14\phantom{\rule{0.2em}{0ex}}\text{eV}-3.62\phantom{\rule{0.2em}{0ex}}\text{eV}=1.52\phantom{\rule{0.2em}{0ex}}\text{eV}\text{.}$

The positive sodium ion and negative chloride ion experience an attractive Coulomb force. The potential free energy associated with this force is given past

${U}_{\text{coul}}=-\frac{k{e}^{2}}{{r}_{0}},$

where $k{e}^{2}=1.440\phantom{\rule{0.2em}{0ex}}\text{eV-nm}$ and ${r}_{0}$ is the distance between the ions.

As the sodium and chloride ions motility together ("descend the potential energy hill"), the forcefulness of allure between the ions becomes stronger. Notwithstanding, if the ions become too close, core-electron moving ridge functions in the two ions brainstorm to overlap. Due to the exclusion principle, this action promotes the core electrons—and therefore the entire molecule—into a college energy state. The equilibrium separation altitude (or bond length) between the ions occurs when the molecule is in its lowest energy country. For diatomic NaCl, this distance is 0.236 nm. (Figure) shows the total energy of NaCl equally a function of the distance of separation between ions.

Graph of free energy versus ionic separation for sodium chloride. Equilibrium separation occur when the total energy is a minimum $\left(-4.36\phantom{\rule{0.2em}{0ex}}\text{eV}\right)$ .

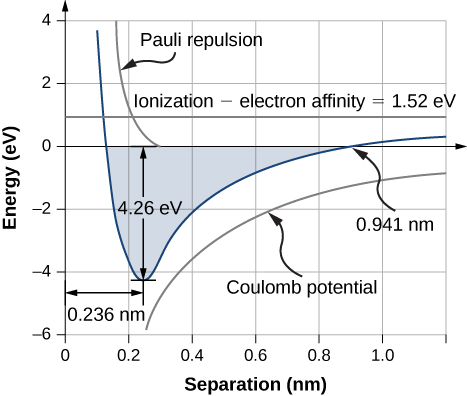
The total free energy required to course a single common salt unit is

${U}_{\text{form}}={E}_{\text{transfer}}+{U}_{\text{coul}}+{U}_{\text{ex}},$

where ${U}_{\text{ex}}$ is the energy associated with the repulsion between core electrons due to Pauli's exclusion principle. The value of ${U}_{\text{form}}$ must be negative for the bond to grade spontaneously. The dissociation free energy is defined every bit the energy required to divide the unit into its constituent ions, written

${U}_{\text{diss}}=\text{−}{U}_{\text{form}}$

Every diatomic formula unit has its own feature dissociation energy and equilibrium separation length. Sample values are given in (Figure).

Bond Length
Molecule	Dissociation Free energy $\left(\text{eV}\right)$	Equilibrium Separation $\left(\text{nm}\right)$ $\left(\text{Bond length}\right)$
$\text{NaCl}$	$4.26$	$0.236$
$\text{NaF}$	$4.99$	$0.193$
$\text{NaBr}$	$3.8$	$0.250$
$\text{NaI}$	$3.1$	$0.271$
$\text{NaH}$	$2.08$	$0.189$
$\text{LiCl}$	$4.86$	$0.202$
$\text{LiH}$	$2.47$	$0.239$
$\text{LiI}$	$3.67$	$0.238$
$\text{KCl}$	$4.43$	$0.267$
$\text{KBr}$	$3.97$	$0.282$
$\text{RbF}$	$5.12$	$0.227$
$\text{RbCl}$	$4.64$	$0.279$
$\text{CsI}$	$3.57$	$0.337$
$\text{H-H}$	$4.5$	$0.075$
$\text{N-N}$	$9.8$	$0.11$
$\text{O-O}$	$5.2$	$0.12$
$\text{F-F}$	$1.6$	$0.14$
$\text{Cl-Cl}$	$2.5$	$0.20$

The Energy of Salt What is the dissociation energy of a salt formula unit (NaCl)?

Strategy Sodium chloride (NaCl) is a salt formed by ionic bonds. The energy change associated with this bond depends on three primary processes: the ionization of Na; the acceptance of the electron from a Na cantlet past a Cl cantlet; and Coulomb attraction of the resulting ions ( ${\text{Na}}^{+}\phantom{\rule{0.2em}{0ex}}\text{and}\phantom{\rule{0.2em}{0ex}}{\text{Cl}}^{\text{−}}$ ). If the ions get also close, they repel due to the exclusion principle (0.32 eV). The equilibrium separation distance is ${r}_{0}=0.236\phantom{\rule{0.2em}{0ex}}\text{nm}\text{.}$

Solution The energy alter associated with the transfer of an electron from Na to Cl is 1.52 eV, every bit discussed before in this section. At equilibrium separation, the atoms are ${r}_{0}=0.236\phantom{\rule{0.2em}{0ex}}\text{nm}$ apart. The electrostatic potential energy of the atoms is

${U}_{\text{coul}}=-\frac{k{e}^{2}}{{r}_{0}}=-\frac{1.44\phantom{\rule{0.2em}{0ex}}\text{eV}·\text{nm}}{0.236\phantom{\rule{0.2em}{0ex}}\text{nm}}=-6.10\phantom{\rule{0.2em}{0ex}}\text{eV}\text{.}$

The total energy difference associated with the formation of a NaCl formula unit is

${E}_{\text{form}}={E}_{\text{xfr}}+{U}_{\text{coul}}+{U}_{\text{ex}}=1.52\phantom{\rule{0.2em}{0ex}}\text{eV}\phantom{\rule{0.2em}{0ex}}+\left(\text{−}6.10\phantom{\rule{0.2em}{0ex}}\text{eV}\right)+0.32\phantom{\rule{0.2em}{0ex}}\text{eV}=\text{−}4.26\phantom{\rule{0.2em}{0ex}}\text{eV}\text{.}$

Therefore, the dissociated energy of NaCl is iv.26 eV.

Significance The formation of a NaCl formula unit of measurement by ionic bonding is energetically favorable. The dissociation energy, or free energy required to divide the NaCl unit into ${\text{Na}}^{+}\phantom{\rule{0.2em}{0ex}}\text{and}\phantom{\rule{0.2em}{0ex}}{\text{Cl}}^{\text{−}}$ ions is iv.26 eV, consistent with (Figure).

Check Your Agreement Why is the potential free energy associated with the exclusion principle positive in (Effigy)?

Information technology corresponds to a repulsive force between core electrons in the ions.

For a sodium ion in an ionic NaCl crystal, the expression for Coulomb potential energy ${U}_{\text{coul}}$ must be modified by a factor known equally the Madelung abiding. This factor takes into account the interaction of the sodium ion with all nearby chloride and sodium ions. The Madelung abiding for a NaCl crystal is about 1.75. This value implies an equilibrium separation altitude between ${\text{Na}}^{+}\phantom{\rule{0.2em}{0ex}}\text{and}\phantom{\rule{0.2em}{0ex}}{\text{Cl}}^{\text{−}}$ ions of 0.280 nm—slightly larger than for diatomic NaCl. Nosotros will return to this point again later.

Covalent bonds

In an ionic bond, an electron transfers from one atom to another. All the same, in a covalent bond, an electron is shared between two atoms. The ionic bonding mechanism cannot explicate the beingness of such molecules as ${\text{H}}_{2}\text{,}\phantom{\rule{0.2em}{0ex}}{\text{O}}_{2},$ and CO, since no separation distance exists for which the negative potential energy of attraction is greater in magnitude than the energy needed to create ions. Agreement precisely how such molecules are covalently bonded relies on a deeper understanding of quantum mechanics that goes across the coverage of this volume, simply nosotros will qualitatively describe the mechanisms in the following department.

Covalent bonds can be understood using the uncomplicated case of a ${\text{H}}_{2}^{+}$ molecule, which consists of one electron in the electric field of two protons. This system tin can be modeled by an electron in a double square well ((Figure)). The electron is equally likely to be found in each well, and then the wave role is either symmetric or antisymmetric about a betoken midway between the wells.

A ane-dimensional model of covalent bonding in a ${\text{H}}_{2}^{+}$ molecule. (a) The symmetric wave function of the electron shared by the 2 positively charged protons (represented by the ii finite square wells). (b) The corresponding antisymmetric wave part.

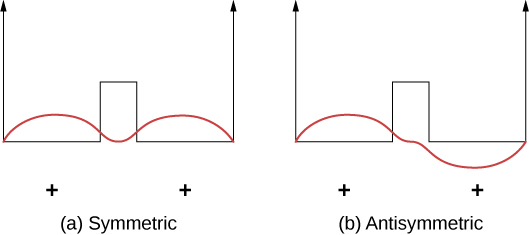
At present imagine that the 2 wells are separated by a large distance. In the ground state, the wave function exists in one of two possible states: either a single positive superlative (a sine wave-similar "hump") in both wells (symmetric case), or a positive peak in one well and a negative height in the other (antisymmetric instance). These states take the same free energy. Still, when the wells are brought together, the symmetric wave role becomes the ground country and the antisymmetric state becomes the first excited state—in other words, the energy level of the electron is split. Find, the infinite-symmetric state becomes the energetically favorable (lower free energy) state.

The aforementioned analysis is appropriate for an electron bound to two hydrogen atoms. Here, the shapes of the ground-state wave functions have the form ${e}^{\text{−}r\text{/}{a}_{0}}$ or ${e}^{\left(\text{−}|x|\text{/}{a}_{0}\right)}$ in one dimension. The energetically favorable, infinite-symmetric state implies a high charge density midway between the protons where the electrons are likely to pull the positively charged protons together.

If a 2d electron is added to this organization to grade a ${\text{H}}_{2}$ molecule, the moving ridge function must depict both particles, including their spatial relationship and relative spins. This moving ridge function must also respect the indistinguishability of electrons. ("If yous've seen one electron, yous've seen them all.") In particular, switching or exchanging the electrons should non produce an appreciable issue, a property called exchange symmetry. Exchange symmetry can be symmetric, producing no change in the wave part, or antisymmetric, producing an overall alter in the sign of the wave function—neither of which is observable.

As we hash out later, the full moving ridge role of two electrons must be antisymmetric on exchange. For example, two electrons bound to a hydrogen molecule can be in a space-symmetric state with antiparallel spins $\left(↑↓\right)$ or space-antisymmetric state with parallel spins $\left(↑↑\right)$ . The country with antiparallel spins is energetically favorable and therefore used in covalent bonding. If the protons are drawn too closely together, notwithstanding, repulsion between the protons becomes important. (In other molecules, this effect is supplied by the exclusion principle.) As a event, ${\text{H}}_{2}$ reaches an equilibrium separation of about 0.074 nm with a binding energy is 4.52 eV.

Quantum mechanics excludes many types of molecules. For case, the molecule ${\text{H}}_{3}$ does not form, because if a tertiary H atom approaches diatomic hydrogen, the wave function of the electron in this atom overlaps the electrons in the other 2 atoms. If all three electrons are in the ground states of their respective atoms, one pair of electrons shares nevertheless quantum numbers, which is forbidden by the exclusion principle. Instead, i of the electrons is forced into a higher energy state. No separation betwixt 3 protons exists for which the total energy change of this procedure is negative—that is, where bonding occurs spontaneously. Similarly, ${\text{He}}_{2}$ is not covalently bonded nether normal weather condition, because these atoms have no valence electrons to share. As the atoms are brought together, the moving ridge functions of the core electrons overlap, and due to the exclusion principle, the electrons are forced into a higher free energy state. No separation exists for which such a molecule is energetically favorable.

Bonding in Polyatomic Molecules

A polyatomic molecule is a molecule fabricated of more than than two atoms. Examples range from a elementary h2o molecule to a complex poly peptide molecule. The structures of these molecules tin ofttimes be understood in terms of covalent bonding and hybridization. Hybridization is a modify in the energy structure of an atom in which mixed states (states that can be written every bit a linear superposition of others) participate in bonding.

To illustrate hybridization, consider the bonding in a simple h2o molecule, ${\text{H}}_{2}\text{O}\text{.}$ The electron configuration of oxygen is $1{s}^{2}2{s}^{2}2{p}^{4}.$ The 1s and 2s electrons are in "airtight shells" and do not participate in bonding. The remaining four electrons are the valence electrons. These electrons can fill six possible states ( $l=1$ , $m=0$ , $±1$ , plus spin up and down). The energies of these states are the same, and then the oxygen atom tin exploit whatever linear combination of these states in bonding with the hydrogen atoms. These linear combinations (which y'all learned about in the chapter on atomic construction) are chosen atomic orbitals, and they are denoted past ${p}_{x},{p}_{y},$ and ${p}_{z}.$ The electron charge distributions for these orbitals are given in (Figure).

The transformation of the electron moving ridge functions of oxygen to ${p}_{x},{p}_{y},$ and ${p}_{z}$ orbitals in the presence of the hydrogen atoms is an case of hybridization. Two electrons are found in the ${p}_{z}$ orbital with paired spins $\left(↑↓\right)$ . One electron is found in each of the ${p}_{x}$ and ${p}_{y}$ orbitals, with unpaired spins. The latter orbitals participate in bonding with the hydrogen atoms. Based on (Effigy), we look the bonding angle for $\text{H—O—H}$ to be $90\text{°}$ . However, if we include the effects of repulsion betwixt atoms, the bond angle is $104.5\text{°}$ . The same arguments can be used to sympathize the tetrahedral shape of methane $\left({\text{CH}}_{4}\right)$ and other molecules.

Summary

Molecules form by two main types of bonds: the ionic bond and the covalent bond. An ionic bond transfers an electron from one atom to some other, and a covalent bond shares the electrons.
The energy alter associated with ionic bonding depends on 3 principal processes: the ionization of an electron from one atom, the acceptance of the electron by the second atom, and the Coulomb attraction of the resulting ions.
Covalent bonds involve space-symmetric wave functions.
Atoms employ a linear combination of wave functions in bonding with other molecules (hybridization).

Conceptual Questions

What is the primary difference between an ionic bond, a covalent bond, and a van der Waals bond?

An ionic bond is formed past the allure of a positive and negative ion. A covalent bond is formed by the sharing of i or more electrons betwixt atoms. A van der Waals bail is formed by the attraction of two electrically polarized molecules.

For the following cases, what type of bonding is expected? (a) KCl molecule; (b) ${\text{N}}_{2}$ molecule.

Draw three steps to ionic bonding.

1. An electron is removed from ane atom. The resulting atom is a positive ion. 2. An electron is captivated from another atom. The outcome atom is a negative ion. 3. The positive and negative ions are attracted together until an equilibrium separation is reached.

What prevents a positive and negative ion from having a zip separation?

For the ${\text{H}}_{2}$ molecule, why must the spins the electron spins be antiparallel?

Bonding is associated with a spatial function that is symmetric under exchange of the two electrons. In this state, the electron density is largest between the atoms. The total role must be antisymmetric (since electrons are fermions), so the spin function must be antisymmetric. In this state, the spins of the electrons are antiparallel.

Problems

The electron configuration of carbon is $1{s}^{2}2{s}^{2}2{p}^{2}.$ Given this electron configuration, what other chemical element might exhibit the same type of hybridization as carbon?

Potassium chloride (KCl) is a molecule formed past an ionic bond. At equilibrium separation the atoms are ${r}_{0}=0.279\phantom{\rule{0.2em}{0ex}}\text{nm}$ apart. Make up one's mind the electrostatic potential energy of the atoms.

$U=-5.16\phantom{\rule{0.2em}{0ex}}\text{eV}$

The electron affinity of Cl is 3.89 eV and the ionization energy of K is 4.34 eV. Use the preceding problem to find the dissociation energy. (Neglect the energy of repulsion.)

The measured energy dissociated energy of KCl is 4.43 eV. Use the results of the preceding problem to determine the energy of repulsion of the ions due to the exclusion principle.

$-4.43\phantom{\rule{0.2em}{0ex}}\text{eV}=-4.69\phantom{\rule{0.2em}{0ex}}\text{eV}+{U}_{\text{ex}},\phantom{\rule{0.2em}{0ex}}{U}_{\text{ex}}=0.26\phantom{\rule{0.2em}{0ex}}\text{eV}$

Glossary

covalent bond: bail formed past the sharing of one or more electrons between atoms

dissociation free energy: amount of energy needed to break apart a molecule into atoms; also, total energy per ion pair to separate the crystal into isolated ions

electron affinity: energy associated with an accepted (bound) electron

equilibrium separation distance: distance between atoms in a molecule

exchange symmetry: how a total wave office changes under the exchange of two electrons

hybridization: change in the energy construction of an cantlet in which energetically favorable mixed states participate in bonding

ionic bond: bond formed by the Coulomb allure of a positive and negative ions

Madelung constant: constant that depends on the geometry of a crystal used to determine the total potential energy of an ion in a crystal

polyatomic molecule: molecule formed of more one atom

van der Waals bond: bond formed by the allure of two electrically polarized molecules

debordwidep1986.blogspot.com

Source: https://opentextbc.ca/universityphysicsv3openstax/chapter/types-of-molecular-bonds/

The Nature of Covalent Bonding 82 Section Review

64 Types of Molecular Bonds

Learning Objectives

Types of Bonds

Ionic bonds

Covalent bonds

Bonding in Polyatomic Molecules

Summary

Conceptual Questions

Problems

Glossary

0 Response to "The Nature of Covalent Bonding 82 Section Review"

Postar um comentário

Iklan Atas Artikel

Iklan Tengah Artikel 1

Iklan Tengah Artikel 2

Iklan Bawah Artikel